Air-Cooled, Picosecond DPSS Lasers
| Laser Model | Output Wavelength |
Pulse Energy (mJ) |
Pulse per second | Pulse Length | Pumping | Cooling |
COMPILER
|
1064 nm | 0.3 | 1000 | 8 ps | Diode | Air |
| 532 nm | 0.18 | 1000 | 7 ps | Diode | Air | |
| 355 nm | 0.06 | 1000 | 6 ps | Diode | Air | |
| 266 nm | 0.16 | 400 | 5 ps | Diode | Air | |
| 213 nm | 0.04 | 400 | 4 ps | Diode | Air | |
Laser for micro-punching machine
|
1064 nm | 1.5 | 2000 | 8 ps | Diode | Air or liquid |
| 532 nm | 0.8 | 2000 | 7 ps | Diode | Air or liquid | |
| 355 nm | 0.3 | 2000 | 6 ps | Diode | Air or liquid | |
| 266 nm | 0.2 | 2000 | 5 ps | Diode | Air or liquid | |
| 213 nm | 0.15 | 2000 | 4 ps | Diode | Air or liquid | |
COMPILER UPGRADE
|
1064 nm | 2 | 1000 | 8 ps | Diode | Air or liquid |
| 532 nm | 1 | 1000 | 7 ps | Diode | Air or liquid | |
| 355 nm | 0.5 | 1000 | 6 ps | Diode | Air or liquid | |
| 1198 nm | 0.3 | 1000 | 32 ps | Diode | Air or liquid | |
| 599 nm | 0.15 | 1000 | 30 ps | Diode | Air or liquid | |
| 299.5 nm | 0.05 | 1000 | 28 ps | Diode | Air or liquid | |
Compiler HPRR
|
1064 nm | 0.15 | 14000 | 8 ps | Diode | Air |
| 532 nm | 0.075 | 14000 | 7 ps | Diode | Air | |
| 355 nm | 0.035 | 14000 | 6 ps | Diode | Air | |
| 266 nm | 0.010 | 14000 | 5 ps | Diode | Air | |
UV-VIS-PICO |
1064 nm | 10 | 200 | 100 ps | Diode | Air or liquid |
| 532 nm | 5 | 200 | 90 ps | Diode | Air or liquid | |
| 355 nm | 3 | 200 | 80 ps | Diode | Air or liquid | |
| 266 nm | 2 | 200 | 75 ps | Diode | Air or liquid |
While high pulse repetition rates provide higher throughput, the high peak power of laser pulses is imperative for cutting different materials with sharper angle, thus significantly reducing material losses and increasing rate of cutting.
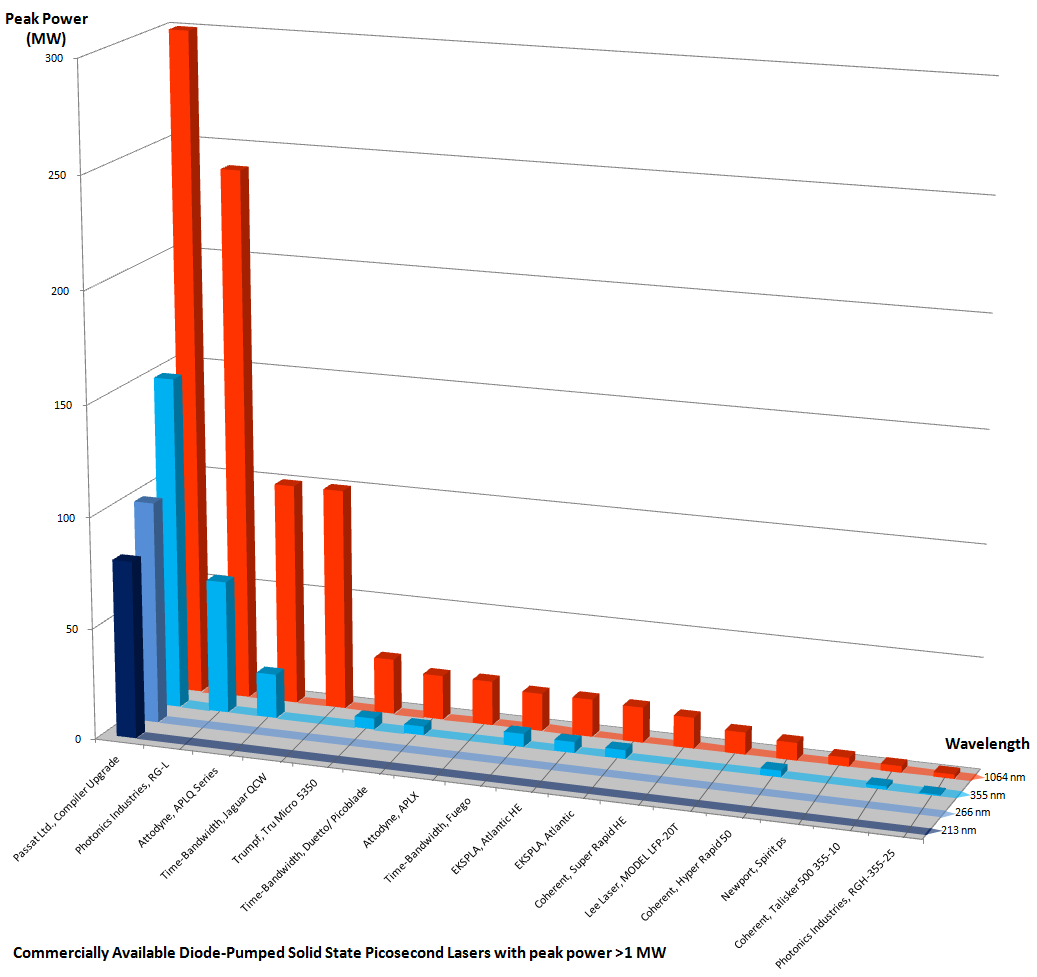
The high peak power is one of the most important features of Passat’s family of picosecond lasers, especially at short UV wavelengths (266 nm, 213 nm).
Picosecond Lasers Articles:
Q-switched lasers: Uses proliferate for high-energy picosecond UV lasers
Materials Processing: Picosecond UV lasers pave the way to new applications
Picosecond Lasers versus Femtosecond Lasers in Micromachining